DataWeave (for Java programmers)
You're a Java programmer trying to gain a better understanding of MuleSoft's DataWeave language? You've come to the right place.

Introduction
The purpose of this post is to fill a gap that exists in the Mule community, answering the question, “I come from a Java background, what do I need to know about DataWeave?” The main difference between Java and DataWeave (DW) is the programming paradigm they fall under; Java falls under the object-oriented paradigm, and DW falls under the functional paradigm. Therefore, this post will help explain the functional programming (FP) concepts that DW implements and how they compare to the imperative/OOP concepts that Java programmers are familiar with. To be clear, you don’t need a solid understanding of what FP, OOP, imperative, etc., is for this post to benefit you. The post will primarily focus on the pragmatic implications of DW’s design as a language, only going into theory when I think it’s especially beneficial to you as a practitioner. This post will assume you have cursory experience with the DW language. Namely, it will expect that you know how to use map and filter. If not, I’d recommend you check out the guides published by Mulesoft for map and filter. The post will start by examining expressions in DW, and how they’re different from statements in Java. Then it will discuss immutable data and pure functions, how they help us reason about code, and how they can make some operations a little more cumbersome. Next, the post will discuss first-class functions, what they are, and how to take advantage. Afterwards, we’ll discuss higher-order functions, what they are, how we use them, and how to make our own. Finally, we’ll discuss lambdas, and how they make functional programming languages like DW easier to work with. Let’s get to it.
Everything is an Expression
In DW, everything is an expression. An expression is a chunk of code that evaluates and returns something. This is opposed to a statement, which can evaluate, but not return anything. Here is an example of a statement in Java:
if(x == 0) {
y = x;
} else {
x = 0;
y = x;
}
Which doesn’t return anything. We couldn’t slap a z = ... in front of the statement and expect to get anything back from it (ignoring the fact that it’s a syntax error and will not compile). Compare this to how DW implements conditional logic:
if (x == 0) 0 else 1
This line of code returns something; it's an expression. I could assign it to a variable:
%var y = if (x == 0) 0 else 1
I’m not the language designer but I’d guess this has something to do with why DW doesn’t have a return keyword. It’s not necessary because everything is an expression, and therefore it is implied that everything returns. So, you can write functions like this:
fun add2(n) =
n + 2
Which might look a little weird to those of you coming from a Java background. There’s no return keyword, so you might ask yourself what does a function return if it contains multiple expressions. It returns the result of evaluating the last expression in the code. For example:
fun add2IfOdd(n) =
if ((n mod 2) != 0)
(n + 2)
else
...
Will return the result of n + 2 when n is odd, but if it’s not, DW will keep evaluating what expressions “...” contains until there is nothing left to evaluate. Finally, it will return whatever value was last returned by the final expression.
As a final example, take printing to the console in Java:
System.out.println(“Hello, world!”);
This is a statement; it doesn’t return anything. Compare this to printing to the console in DW:
var onePlusOne = log("the result of 1 + 1", 1 + 1)
This will do two things, print “the result of 1 + 1 - 2” to the console, and return the value 2 from the log function. The variable assignment is not necessary to use log, it’s just put there to illustrate that log returns a value that you can use later. If you’re curious about how log works in action, check out my post about debugging DW code, here.
The lesson here is to remember that every block of code in DW is an expression, and therefore returns a value. This is a significant break from Java-esque paradigm where statements are also available.
Immutable Data and Pure Functions
Immutable data is a feature of DW that might not be immediately apparent to developers coming from a Java background. For example, in the following script:
%dw 2.0
output application/json
var input = [1,2,3,4,5,6]
---
input filter $ > 3
// Output: [4,5,6]
you might think the filter function removed the first three values from the input array, and just returned the modified array. However, since DW has immutable data, you cannot remove values from an existing array. Instead, a better way to think about this is DW is creating a new array without the first three values of the input array. You can see this here:
%dw 2.0
output application/json
var input = [1,2,3,4,5,6]
var big = input filter $ > 3
---
input
// Output: [1,2,3,4,5,6]
For those of you who learn better visually, this representation might better help explain what’s going on. DW is essentially passing each value through the filter to determine if it makes it into the output array:
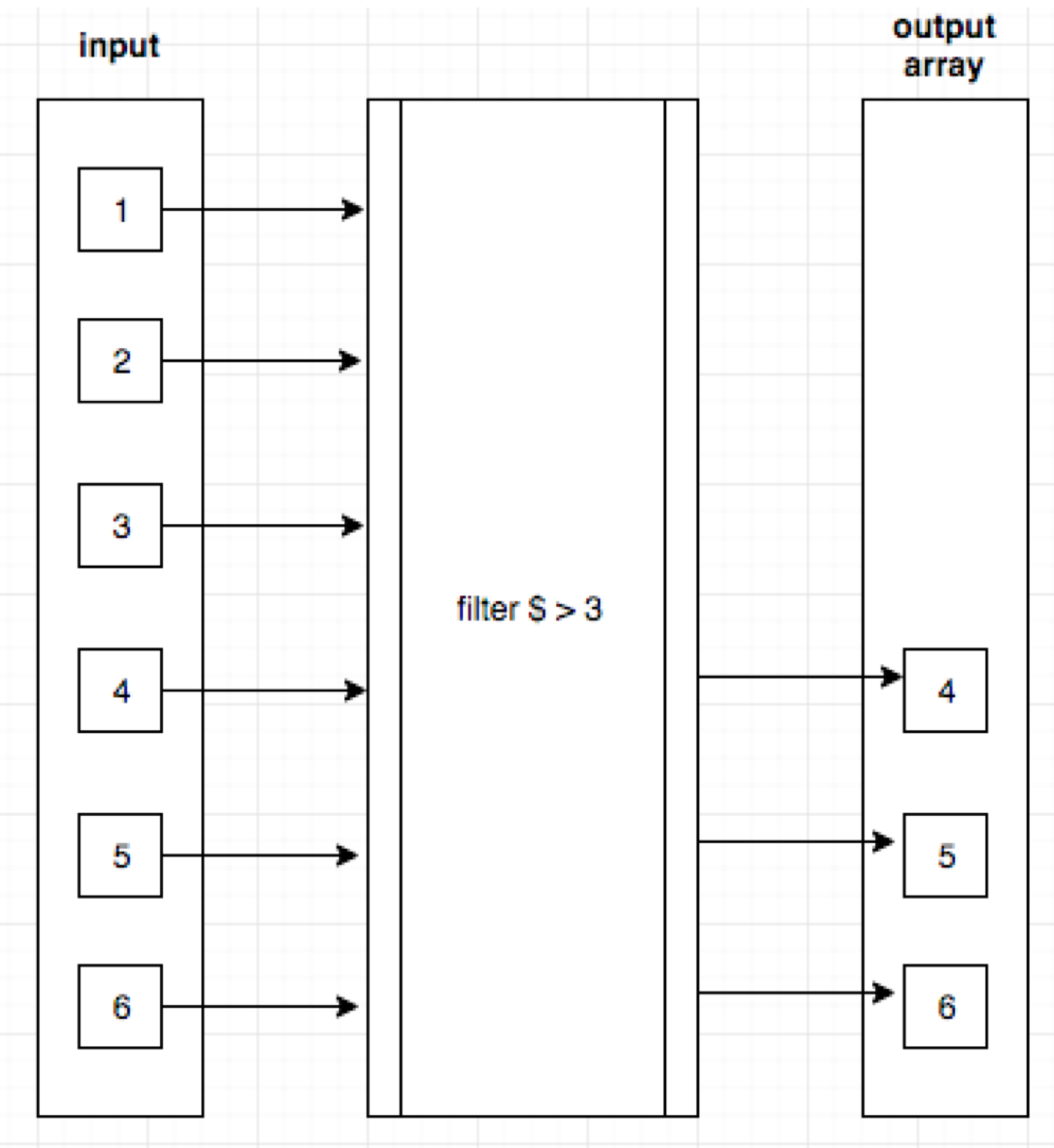
This might seem like a “6 or one-half dozen” situation, but the implications are very important to understand if you ever wish to write any code in DW that isn’t trivial. In terms of how it will affect the design of your DW code vs Java code, there are two big consequences that will affect you day-to-day: imperative looping constructs like for are gone (they rely on modifying a variable so that the loop terminates), and values will never be modified (this gives us pure functions, more on them later).
No more imperative looping constructs ends up being not as disruptive as you might think, as the pattern of looping is abstracted away enough by functions you’ll use every day, like map and filter. However, sometimes map and filter won’t be the right tool for the job. Luckily, reduce is always available, and lastly, recursive functions calls (i.e. functions that call themselves). As a warning, situations where you will need to use reduce or recursion will become disruptive until you become more comfortable with them. Practice makes perfect, so check out some of the DataWeave practice problems I've put together and give them a try here.
The fact that data cannot be modified almost always benefits us in that it allows us to more easily reason about the code, because we don’t have to wonder whether a function will modify a variable that we pass to it. To state it as simply as possible, code with immutable data is easier to reason about because you can substitute any expression with the result of the expression. This is called referential transparency. A very nice side effect of immutable data is something called pure functions. Pure functions are functions that return the same output when given the same input no matter what. This gives our code a math-like quality when it comes to reasoning about how it works. With the mathematical expression (1 + 2) * 3, we can substitute 3 for (1 + 2) to give us the simpler expression 3 * 3. In DW, with the following code it works the same way:
%dw 2.0
output application/java
fun add2(n) = n + 2
fun multiplyBy3(n) = n * 3
---
multiplyBy3(add2(1))
We can confidently substitute the expression add2(1) with the value 3, relieving ourselves of the mental burden of needing to understand how that function works anymore in the context of the larger goal. Now we’d only need to understand how multiplyBy3(3) works. This idea probably seems trivial in this context; after all, how hard is it to reason about simple arithmetic? However, this idea scales nicely as our DW scripts become more complicated. A script could call 10 different functions, but we can effectively look at the script at a macro level, saying that instead of an orchestration of 10 individual functions, it’s instead one huge function and if x goes into this big function we will get y from it every time, or we can zoom in a bit to a more micro level and make the same kinds of assertions against individual functions and expressions. This the power of pure functions and immutable data.
I’m sure you noticed I said this idea almost always benefits us; we don’t get this powerful ability to easily reason about our code for nothing. One downside is that it forces you to think about how your programs work in a different way, and this takes time to get comfortable with. The other downside is that sometimes it can make cases that would be easy to implement in imperative languages tedious, e.g., incrementing a value in an existing object. In Java, you can do this in a single line of code if you chose not to use a temporary variable:
// The variable m could be represented as {“one”: 1, “two”: 2}
m.put(“one”, map.get(“one”) + 1);
// Results in m == {“one”: 2, “two”: 2}
To achieve a similar result in DW, we need to create a new object from the existing object, where all the fields are the same except the target value, which is incremented by one:
%dw 2.0
output application/json
var m = {
'one': 1,
'two': 2
}
---
m mapObject (
if (($$ as String) == 'one')
{
($$): $ + 1
}
else
{
($$): $
}
)
// Output:
// {
// ‘one’: 2,
// ‘two’: 2
// }
That’s 7 lines of DW to 1 line in Java (of course we could compress all the DW code into one line, but who wants to read that?). This case is an outlier, however, so while we are writing more DW code than we would need to achieve the same result in Java, on average we’ll will wind up writing significantly less DW code than we would need to do the same thing in Java (this is a huge win as well because less code means less places for bugs to hide). For this reason, I’ve found over time that I don’t mind the tradeoff at all. Occasional inconveniences are a small cost to pay for the constant ability to more easily reason about how code is supposed to work.
Now that we’ve covered expressions, immutable data, and pure functions, you could probably stop here and go about the rest of your Mule career writing DW code that is great. You now know that instead of thinking about code in terms of how you can modify existing data to get what you want, in DW, you instead need to think about code in terms of how to take existing data and create new data from it to get what you want. At this point, I’d recommend you take this knowledge with you and educate yourself on the internal mechanics of map, filter, and reduce.
First-Class Functions
In DW, functions are first-class citizens. This means that we can use them in the same way we do arrays, objects, and primitives. We can assign them to variables, pass them to functions, return them from functions, add them to arrays, etc. This is what allows for functions like map, filter, and reduce to take other functions as parameters with minimal boilerplate code. Here’s a pedagogical example:
%dw 2.0
output application/json
var input = [1,2,3,4,5,6]
fun even(n) =
(n mod 2) == 0
var isEven = even
---
input filter isEven($)
In the above example, we assign the function even to the variable isEven, and pass that variable to the filter function, leveraging two pieces of functionality we gain from first-class functions. Coming from a Java background myself, I found calling variables as functions a bit odd. Just remember, this isn’t too different from the familiar Java concept of assigning an array to a variable, x, and getting the value at the first index, x[0].
First-class functions are typically a pain-point for programmers with a Java background, because they’re a feature that the language doesn’t support. If you’re a lifetime Java programmer, this concept of functions running around without having their hands held by classes is unfamiliar. As a Java programmer, you’re mostly passing around data, not functionality. If you’ve done any programming in JavaScript (I hope this assumption isn’t too far off, as the majority of programmers in the world have some experience with JS), you’ve probably dealt with first-class functions before:
[1,2,3,4,5].forEach(function(n) {
console.log(n + 1);
});
In this case, the forEach function is passed a function as its sole argument.
You won’t find much in the Mule documentation on DW about first-class functions (or really any of the FP concepts of the language, for that matter), but there are a ton of learning materials centered around them for other languages. Keep in mind, you’re better off in the long-run investing time in trying to understand the functional concepts that DW leverages, not necessarily DW as a language, because these concepts apply to almost all languages that adhere to the FP paradigm in one way or another including much of the stream functionality added with Java 8. On that note, I’d encourage you to learn about first-class functions, and higher-order functions (next section) using a more popular language with ample documentation and blog posts, like JavaScript. JavaScript shares a few important things with DW, like first-class functions and being a dynamic language (more or less), however, JavaScript has mutable data by default, so be aware of this when learning through it. I’m confident that the functional concepts you learn in JavaScript will easily carry over to DW. I first learned about functional programming using JavaScript, and then brought those ideas into my Python code, and everything I learned there allowed me to more quickly pick up and identify the advantages of the DW language in the context it lives in.
Higher-Order Functions
First-class functions enable us to create higher-order functions. A higher-order function is a function that takes another function as input, returns a function as output, or both. Higher-order functions wind up being a powerful tool in terms abstraction, separation of concerns, and ultimately code reuse, much like classes. In the case of the map function, it separates the concerns of iteration over an array and grabbing every value with how to map those values to the output array, which you supply on the right side of the function call.
I like to use the example of counting things in an array to illustrate this separation of concerns. For example, what if you had a requirement that asked you to determine the count of numbers in an array greater than 100? We’ll implement this using filter and sizeOf, although keep in mind this is a great use case for reduce as well (more info on that here):
%dw 2.0
output application/json
var input = [98,99,100,101,102]
fun countGreaterThan100(arr) =
sizeOf(arr filter $ > 100)
---
countGreaterThan100(input)
// Output: 2
Then you get another requirement where you need to get the count of strings in an array that match an ID provided in a flowVar. You might be eyeing your countGreaterThan100 function and trying to figure out a way you could make it more general-purpose, so that is works for both cases. But you see that it’s counting based off numeric comparisons, and now you need to compare strings. Eventually you get discouraged and implement this function:
fun countOfIdMatches(arr) =
sizeOf (arr filter $ == flowVars.id)
But notice the similarities:
fun countGreaterThan100(arr) =
sizeOf(arr filter $ > 100)
fun countOfIdMatches(arr) =
sizeOf (arr filter $ == flowVars.id)
We pass in an array, we’re using filter and sizeOf in the exact same way, and the shape of them is almost identical. With so many similarities identified, chances are we’ll be able to abstract those similarities out into their own function. But first we need to identify the differences so we can try to pull them out and make the function more general. You may have noticed that the only thing that’s meaningfully different is how to filter the array, which is determined by an expression that evaluates to true or false. What if we could pass in that expression? You can, just wrap it in a function and call it within the counting function with the appropriate arguments to determine whether to increment the counter. Then you could use it to count things dealing with strings, numbers, objects, arrays, etc.:
fun countBy(arr, fn) =
sizeOf (arr filter fn($))
fun greaterThan100(n) = n > 100
fun idMatch(id) = id == flowVars.id
var over100 = countBy([98,99,100,101,102], greaterThan100)
var idMatches = countBy([“1”, “2”, “2”, “3”, “2”], idMatch)
This is how you can use higher-order functions to create utility functions that will likely find use across multiple projects.
Lambdas
Lambdas are just a fancy way of saying functions that don’t have a name. These are also called anonymous functions, function literals, and unnamed functions. Here’s what they look like in DW:
((n) -> n + 1)
You define your input parameters in parenthesis, add an arrow, then define the body of the function which defines what to do with the parameters. Then you wrap the whole thing in parenthesis. In this case, we have a function that takes in a single parameter, n, and returns the result of adding n + 1. You can take in more than one parameter to your function, if necessary:
((n, m) -> n + m)
Lambdas are rarely necessary in the sense that we can get along just fine without them, because you can always define a function before you use it. However, lambdas allow us to create functions on the fly. This allows us to more easily work with higher-order functions without any boilerplate code. If you’ve been using filter, you’ve probably been using lambdas without knowing it:
[“foo”,”bar”,”foo”,”foo”,”bar”] filter $ == “foo”
Here, $ == “foo” is a lambda. You might be thinking to yourself “Yes, I’ve done that before, but the syntax doesn’t match what you said earlier.” You’re correct. What I just showed is a syntactic convenience for this:
[“foo”,”bar”,”foo”,”foo”,”bar”] filter ((str) -> str == “foo”)
Where $ in the previous code just refers to the current value of the iteration. Just keep in mind that $ (and $$ for some functions) is only available for built-in DW functions, not functions that you define.
Let’s see how we’d use the countBy function in our previous section with a lambda instead of a previously defined function:
fun countBy(arr, fn) =
arr reduce ((e, count=0) ->
if (fn(e))
count + 1
else
count
)
---
countBy([1,2,3,4,5], ((n) -> n > 3))
// Output: [4,5]
So, we need to add an input parameter, fn, that will take in our function that declares when to increment the counter. Then we will replace the conditional section of the when expression with a call to fn, being sure to pass to it the current value of the iteration, which we’ve defined as e, for “element” as it could be anything. And that’s it!
Conclusion
In summary, we went over expressions, immutable data, pure functions, functions as first-class citizens, higher-order functions, and lambdas. We discussed what each of these points is, how they require different thinking than the OO thinking we’re comfortable with, and how they work together to enable DW to excel at the task it’s set out to do. The goal of this post was to explain these concepts to existing Java programmers, but please understand that this high-level shift in the way you think about how your code works and how it’s structured is not going to happen overnight. But if you’re diligent, and you work a little bit at it each day, you’ll start to see the power of DW’s design, as well as all languages that adhere to the FP paradigm.